カバリエリの原理

これも（公立の）学校では余り教えない原理の一つ。
コウが通っていたマニアック数学塾のテキストに載っているのを見つけ、懐かしかったので取り上げた。

カバリエリの原理

　　　　　二つの立体を一定の平面に平行な平面で切ったとき、切り口の面積の比が常に等しければ、この二つの立体の体積の比は等しい。　　　・・・（☆）
　　　　　（切り口の面積が等しければ、それらの立体の体積は等しい）

　　　　　　　　　　　　　　　fig.1

これも「鳩の巣原理」同様、当たり前のように思える。

例えば、段ボールを面積が同じになるように切り出し、同じ枚数重ねると体積は同じになっている。

　　　　　　　　　　　　　　　fig.2

ここでfig.1の立体と異なっているのは、段ボールの厚みによりfig.2の立体はfig.1の立体ほど側面が「なめらか」でない事だ。
そこで、段ボールをどんどん薄いモノに換えていくと、限りなくfig.1の立体のように「なめらか」になっていく。

そう、これは微積のアイデアだ。
実際、カバリエリは「平面図形は無数の線分から成り、立体は無数の面から成る」と考え、これら線分や面を「不可分量」（indivisible）と呼んだ。
微積のアイデアの萌芽は遙か紀元前１９世紀頃の古代エジプトまで遡るが、その後、アルキメデスや祖沖之（５世紀：中国）、ハイサム（１１世紀：イスラム）、
バースカラ（１２世紀：インド）、関孝和（１７世紀：日本）らにより連綿と受け継がれた。
カバリエリは１７世紀のイタリアの数学者で、カバリエリが活躍した数十年後にはニュートン・ライプニッツにより微分積分学は確立する。

（☆）のカバリエリの原理は立体についての記述だが、次元を一つ下げて（つまり微分して）も成り立つ。
　　　　　2つの平面図形を一定の直線に平行な任意の直線で切ったとき、切り口の線分の長さの比が常に等しければ、この二つの平面図形の面積の比は等しい。

カバリエリの原理を使って、球の体積を求めてみよう。
前提として、錐体の体積は柱体の体積の1/3である事は既知とする。
（例えば、同じ底面積・高さの円錐は円柱の1/3の体積である）

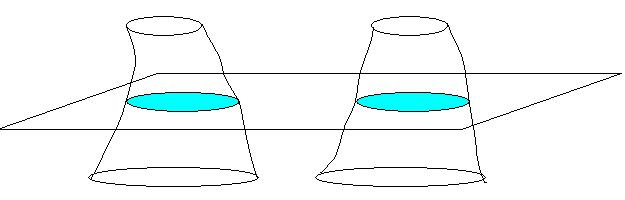
半径ｒの球と、半径ｒで高さ2ｒの円柱から半径ｒで高さｒの円錐を２つ取り去った立体を考える。（fig.3）

　　　　　　　　　　　　　　　fig.3

すると、同じ平面の切り口（それぞれの「青い」部分）の面積は等しい。

実際に計算してみよう。
球の中心からｈの高さでの切り口は下図の青い線になる。

　
　　　　　　　　　　　　　　　　fig.4

左の円は、半径が $sqrt{r^2-h^2}$ なので、面積は ${\pi}(r^2-h^2)$
右のドーナツ形は、半径ｒの円から半径ｈの円をくり抜いたモノなので、面積は ${\pi}(r^2-h^2)$
つまり、この切り口となる平面を上から下までスキャンしたとき、左右の切り口の図形の面積は常に等しい。
よって、カバリエリの原理より、fig.3の球の体積は右の立体の体積に等しい。

では、右の立体の体積を求めてみよう。

先ず、半径ｒで高さが２ｒの円柱の体積は　　　 $2{\pi}r^3$ 　・・・（１）
くり抜く円錐１つの体積は、半径ｒで高さがｒなので　　　 ${\pi}r^3\over 3$ 　これが２つなので　　 $2{\pi}r^3\over 3$ 　・・・（２）
よって右側の立体の体積は　（１）−（２）なので　　　 $4{\pi}r^3\over 3$
つまり、これが半径ｒの球の体積となる。

ちなみに、「錐体の体積が柱体の体積の1/3」（★）なのは、次のように確認できる。

　　　　　　　　　　　　　　　　　fig.5

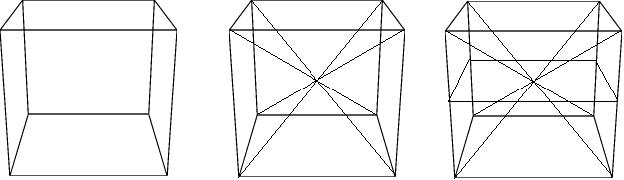
先ず、一辺が2rの立方体を考える（左の図）。その立方体を真ん中の図のように切り分けて、６つの四角錐を作る。
この四角錐は一辺が2ｒの正方形が底面で高さがｒになっている。
ここで一辺が2rの立方体の真ん中を水平に切ると（右の図）、一辺が2rの正方形を底面とする高さがｒの直方体の中に、
一辺が2ｒの正方形が底面で高さがｒの四角錐が３つ入っていることになる。
よって、底面が同じ（一辺が2rの正方形）で高さが同じ（ｒ）四角錐の体積は直方体の体積の1/3になっている。
後はカバリエリの原理により、どの様な形の底面であっても上記の関係性は保たれる。
よって（★）の命題は証明された。